In this section, we will explore the unique properties of isosceles triangles. Isosceles triangles are geometric shapes with fascinating properties that make them essential in the study of triangles. From their angle measurements to their classification and various formulas, understanding the properties of isosceles triangles is crucial for mastering geometry.
Isosceles triangles, like other triangles, have angles and measurements that define their structure. By examining these properties, we can uncover the relationships and patterns that exist within isosceles triangles. This knowledge not only expands our understanding of geometry but also enhances our problem-solving skills.
Key Takeaways:
- Isosceles triangles possess two equal sides and two equal angles, making them distinct in shape.
- The angle measurements of isosceles triangles are interconnected, with the base angles being congruent and the vertex angle being different.
- Formulas such as the Pythagorean Theorem and the Law of Cosines can be used to calculate unknown measurements of isosceles triangles.
- Isosceles triangles can be classified based on their angles and side lengths, providing a deeper understanding of their characteristics.
- Understanding the properties of isosceles triangles is essential for solving geometry problems and exploring the relationships between different geometric shapes.
What is an Isosceles Triangle?
An isosceles triangle is a geometric shape that possesses two equal sides. This special property sets it apart from other triangles, making it an intriguing figure in the field of geometry.
The isosceles triangle, as the name suggests, consists of two sides with equal lengths, known as the legs or the lateral sides. The third side, known as the base, may have a different length. The angle opposite the base, referred to as the vertex angle, is typically larger than the two base angles.
Isosceles triangles have several unique characteristics that make them significant in the study of geometric shapes. These triangles exhibit symmetry, where the base angles are always congruent, meaning they have the same measure. The vertex angle, on the other hand, varies but is always smaller than the sum of the base angles.
The symmetrical nature of isosceles triangles allows mathematicians to apply various formulas to calculate missing angles and side lengths. These formulas include the Pythagorean Theorem, trigonometric functions, and the properties of similar triangles.
“The isosceles triangle is a fascinating geometric shape that captivates mathematicians and students alike. Its symmetry and distinct properties offer a wealth of opportunities for exploration and understanding in the realm of geometry.”
| Properties of Isosceles Triangles | |
|---|---|
| Angle Measurements | The base angles are congruent. |
| The vertex angle is smaller than the sum of the base angles. | |
| The sum of all angles in an isosceles triangle is always 180 degrees. | |
| Side Lengths | The legs are congruent. |
| The base can have a different length. | |
| The sum of the lengths of any two sides is always greater than the length of the third side. |
Understanding the properties and characteristics of isosceles triangles is crucial for solving geometrical problems and applications. Whether it’s determining unknown angles or sides, identifying congruent triangles, or analyzing the symmetry of shapes, isosceles triangles play a vital role in various mathematical scenarios.
Angle Measurements of Isosceles Triangles
In this section, we will explore the angle measurements of isosceles triangles, one of the fundamental aspects of their properties. Understanding these angle measurements is crucial in analyzing and solving problems related to isosceles triangles.
Relationship between Base Angles and Vertex Angle
An isosceles triangle has two congruent sides, known as the legs, and a third side, known as the base. The two angles opposite the legs are called the base angles, while the angle formed by the two legs is known as the vertex angle.
The base angles of an isosceles triangle are always congruent. This means that the measurement of each base angle is equal to half the difference between 180 degrees and the measurement of the vertex angle.
For example, if the vertex angle of an isosceles triangle measures 70 degrees, each base angle would measure (180 – 70) / 2 = 55 degrees.
Calculating Angle Measurements
There are several formulas that can be used to calculate the angle measurements of an isosceles triangle:
- Measurements of congruent base angles: The measurement of each base angle is given by: (180 – measurement of vertex angle) / 2.
- Vertex angle based on base angle: The measurement of the vertex angle is given by: 180 – (2 * measurement of base angle).
- Sum of all three angles: The sum of the measuremements of all three angles in an isosceles triangle is always 180 degrees.
Visual Representation
Below is a visual representation of an isosceles triangle, highlighting the relationship between the base angles and the vertex angle:
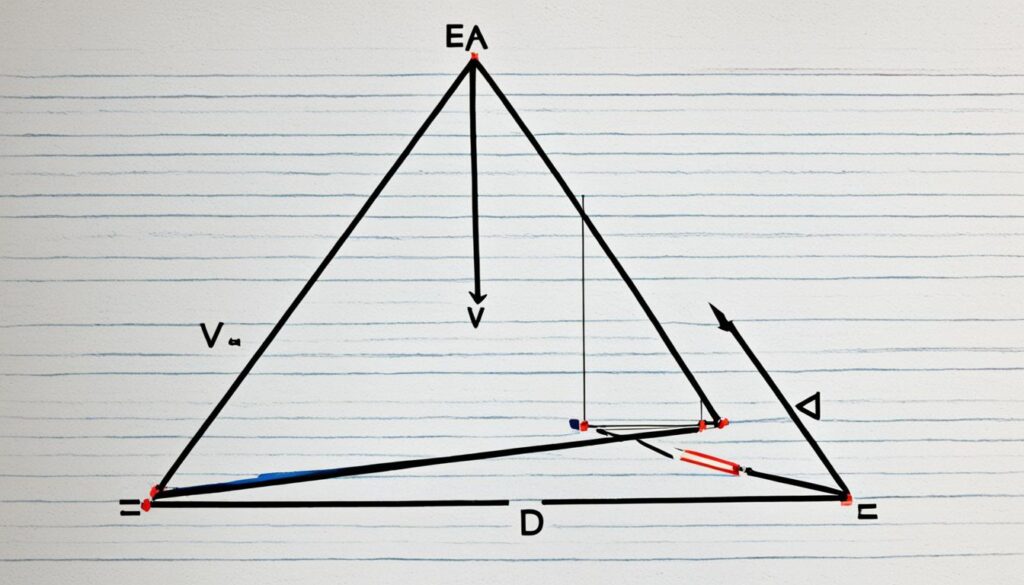
Classification of Isosceles Triangles
When it comes to isosceles triangles, understanding their classification based on angles and side lengths is key to gaining a comprehensive knowledge of geometric shapes. By exploring the relationship between isosceles triangles and other triangle types, such as equilateral triangles, we can appreciate the distinct characteristics that define each classification.
An isosceles triangle is defined as having two equal sides, known as legs, and two equal angles opposite those sides, called base angles. While the base angles are always congruent, the vertex angle, formed by the remaining side, can vary in measurement.
Classification of isosceles triangles is primarily based on the measures of the base angles, which determine the overall shape and properties of the triangle. Let’s explore the different categories:
1. Acute Isosceles Triangle
An acute isosceles triangle is when both base angles are less than 90 degrees. This classification represents a triangle that has a sharp, pointed vertex angle, indicating a narrower shape.
2. Right Isosceles Triangle
In a right isosceles triangle, one of the base angles measures exactly 90 degrees, forming a right angle. This classification results in a triangle with a vertex angle of 45 degrees, creating a balanced and symmetrical shape.
3. Obtuse Isosceles Triangle
An obtuse isosceles triangle has one base angle greater than 90 degrees. This classification produces a triangle with a wider, more open vertex angle, giving it a flatter appearance.
By classifying isosceles triangles based on their angles, we can gain insights into their unique properties and further understand their relationship with other geometric shapes. This knowledge is invaluable in geometry, as it allows us to solve problems, make calculations, and apply formulas with accuracy and precision.
Conclusion
In this article, we have explored the fascinating properties of isosceles triangles and their significance in the realm of geometry. By understanding the unique characteristics and measurements of isosceles triangles, we gain valuable insights into the broader field of triangle properties and geometric shapes.
Through our exploration, we have learned that isosceles triangles have two equal sides, which sets them apart from other triangles. This property enables us to apply specific formulas and calculations to determine angles and side lengths. By mastering these formulas, we can analyze and solve various geometric problems involving isosceles triangles.
Furthermore, the classification of isosceles triangles plays a crucial role in geometry. By studying their angles and side lengths, we can categorize them and understand their relationships with other types of triangles, such as equilateral triangles. This classification framework provides a solid foundation for further exploration of geometric shapes and their properties.
Overall, our journey through isosceles triangle properties has shed light on the beauty and intricacy of geometric shapes. By grasping the concepts of triangle angles, measurements, and formulas, we can unlock a deeper understanding of geometry and its practical applications in various fields.
FAQ
What is an isosceles triangle?
An isosceles triangle is a geometric shape that has two equal sides. The third side, called the base, is typically shorter or longer than the equal sides.
What are the properties of an isosceles triangle?
Isosceles triangles have several unique properties. The base angles, formed between the base and each equal side, are always congruent. The vertex angle, formed opposite the base, is always larger than the base angles.
How do you calculate the angles of an isosceles triangle?
To calculate the angle measurements of an isosceles triangle, you can use several formulas. The base angles can be found by dividing the sum of all angles by 2 and subtracting the vertex angle. The vertex angle can be found by subtracting the sum of the base angles from 180 degrees.
Can an isosceles triangle be equilateral?
Yes, an isosceles triangle can also be equilateral if all three sides are equal in length. In this case, all angles of the triangle would be congruent and measure 60 degrees each.
How is an isosceles triangle classified?
Isosceles triangles can be classified based on their angles and side lengths. If all three angles are acute (less than 90 degrees), it is an acute isosceles triangle. If one angle is obtuse (greater than 90 degrees), it is an obtuse isosceles triangle. If all three angles are right angles (90 degrees), it is a right isosceles triangle.