Welcome to our exploration of parallelograms, one of the fascinating shapes in geometry. Parallelograms are a type of quadrilateral that possess unique properties, making them an intriguing subject to study. In this section, we will dive into the fundamental aspects of parallelograms, including their angles, sides, area, and perimeter. By understanding these properties, you will gain a solid foundation in the geometry of parallelograms.
Key Takeaways
- Parallelograms are a type of quadrilateral with distinct properties.
- Understanding the angles and sides of a parallelogram is essential for solving geometry problems.
- The area and perimeter of a parallelogram can be calculated using specific formulas.
- Parallelograms have opposite sides that are parallel and equal in length.
- By mastering the properties of parallelograms, you will develop a strong foundation in geometry.
Understanding Parallelograms
In this section, we will provide a comprehensive understanding of parallelograms. A parallelogram is a type of quadrilateral, a polygon with four sides. What sets parallelograms apart from other quadrilaterals is their unique set of properties that define their shape and structure. Let’s dive deeper into these properties and explore what makes parallelograms fascinating.
“A parallelogram is a four-sided polygon with opposite sides that are parallel and equal in length.”
As mentioned earlier, one of the key properties of a parallelogram is its set of parallel sides. This means that opposite sides of a parallelogram never intersect and are always of equal length. This creates a distinct symmetry that defines the shape of the parallelogram.
Additionally, parallelograms have equal opposite angles. This means that the angles formed by the intersection of the parallelogram’s sides are equal in measurement. These angles are the interior angles of the parallelogram and play a crucial role in understanding its properties.
Let’s summarize the properties of a parallelogram in a table:
| Property | Description |
|---|---|
| Parallel sides | Opposite sides are parallel and equal in length |
| Equal opposite angles | Angles formed by the intersection of sides are equal |
Visualizing Parallelograms
As shown in the image, we can observe the parallel sides and equal opposite angles that define a parallelogram. These properties are consistent across all parallelograms, regardless of their size or orientation.
Now that we have a solid understanding of what parallelograms are and their fundamental properties, we can proceed to explore the angle properties of parallelograms in the next section.
Angle Properties of Parallelograms
In this section, we will explore the angle properties of parallelograms and uncover their significance in solving geometry problems. By understanding the relationships between the various angles within a parallelogram, we can gain valuable insights into its properties and applications. Let’s dive in!
Opposite Angles
One of the essential angle properties of a parallelogram is the presence of opposite angles. Opposite angles in a parallelogram are congruent, meaning they have the same measure. This property can be represented as:
∠A = ∠C and ∠B = ∠D
By knowing the measure of one angle, we can determine the measure of the opposite angle, providing us with a useful tool for solving geometry problems.
Consecutive Angles
Another important angle property of parallelograms is the relationship between consecutive angles, which are angles that share a side. Consecutive angles in a parallelogram are supplementary, meaning their measures add up to 180 degrees. This property can be represented as:
∠A + ∠B = ∠B + ∠C = ∠C + ∠D = ∠D + ∠A = 180°
Understanding the supplementary nature of consecutive angles allows us to determine the measure of one angle when the measure of the other angle is known.
Diagonal Angles
When a diagonal is drawn within a parallelogram, it creates four new angles. These diagonal angles have unique properties within the parallelogram:
- The diagonally opposite angles are congruent:
- The adjacent diagonal angles are supplementary:
∠A = ∠C and ∠B = ∠D
∠A + ∠C = ∠B + ∠D = 180°
These properties of the diagonal angles provide valuable insights into the symmetry and relationships within a parallelogram.
| Angle Property | Summary |
|---|---|
| Opposite Angles | Congruent |
| Consecutive Angles | Supplementary |
| Diagonal angles (opposite) | Congruent |
| Diagonal angles (adjacent) | Supplementary |
Understanding the angle properties of parallelograms is crucial for solving geometry problems involving these fascinating shapes. By leveraging the relationships between opposite, consecutive, and diagonal angles, we can derive valuable insights and solutions.
Side Properties of Parallelograms
When it comes to parallelograms, the properties of their sides play a crucial role in defining the shape and structure. Let’s explore the relationships between the different sides of a parallelogram and understand how these properties contribute to its overall geometry.
Opposite Sides of Parallelograms
One of the key properties of a parallelogram is that its opposite sides are equal in length. In other words, if we label the sides as a, b, c, and d, then a = c and b = d. This property ensures that the parallelogram remains balanced and symmetrical.
Parallel Sides
Another important property of parallelograms is that their opposite sides are parallel. This means that a is parallel to c and b is parallel to d. The parallel sides help define the overall shape of the parallelogram and allow for unique geometric properties.
“The opposite sides of a parallelogram are equal in length, and the parallel sides contribute to its balanced structure.” – Geometry Guru
Diagonals of Parallelograms
The diagonals of a parallelogram are the line segments that connect the opposite corners. These diagonals also exhibit interesting properties. The main property of the diagonals is that they bisect each other. In other words, the point of intersection divides each diagonal into two equal parts.
Furthermore, the diagonals of a parallelogram also divide it into four congruent triangles. This property allows for additional insights into the shape and symmetry of the parallelogram.
“The diagonals of a parallelogram bisect each other and divide it into four congruent triangles.” – Geometry Expert
A Visual Representation
To better understand the side properties of parallelograms, take a look at the diagram below:
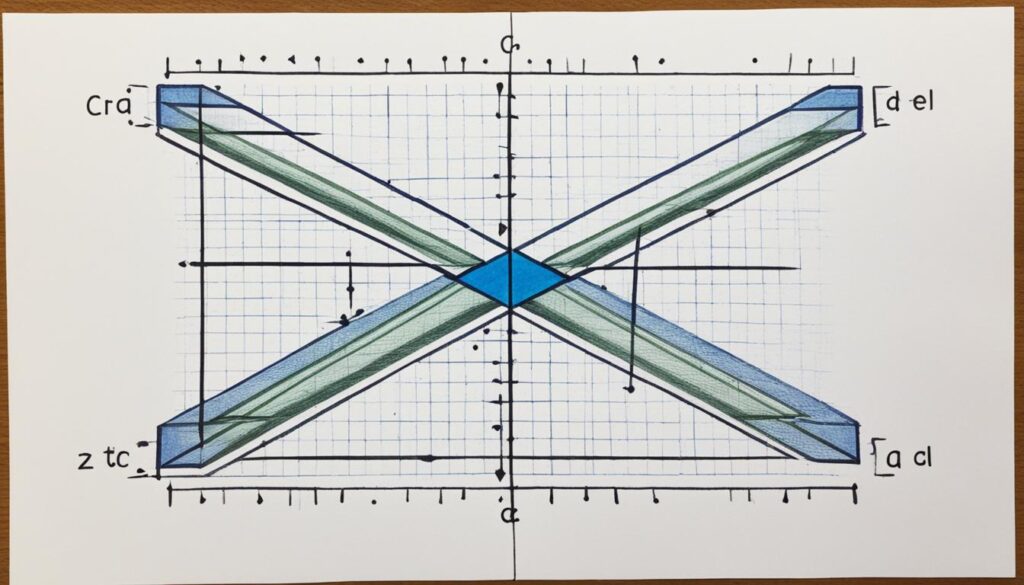
| Property | Description |
|---|---|
| Equal Opposite Sides | The opposite sides of a parallelogram are equal in length. |
| Parallel Sides | The opposite sides of a parallelogram are parallel to each other. |
| Bisecting Diagonals | The diagonals of a parallelogram bisect each other. |
| Congruent Triangles | The diagonals of a parallelogram divide it into four congruent triangles. |
By understanding the side properties of parallelograms, you can unlock the door to solving various geometry problems and uncovering fascinating patterns within this unique shape.
Calculating the Area of a Parallelogram
In the previous sections, we explored the properties and geometry of parallelograms, focusing on angles, sides, and their overall structure. Now, let’s shift our attention to calculating the area of a parallelogram, an essential concept in geometry.
The formula to find the area of a parallelogram is straightforward:
Area = base × height
Where the base represents the length of any of the parallel sides, and the height represents the perpendicular distance between the parallel sides.
Let’s take a look at an example to better understand how to calculate the area of a parallelogram:
Example:
Consider a parallelogram with a base of 6 units and a height of 4 units.
Using the formula, the area can be calculated as follows:
Area = 6 units × 4 units = 24 square units
So, the area of the given parallelogram is 24 square units.
It’s important to note that the units used for the base and height measurements must be the same to ensure consistency when calculating the area.
Calculating Area with Different Measurements
In some cases, the base and height of a parallelogram may be given in different measurements, such as inches and centimeters. To find the area, you must convert the measurements to the same unit before applying the formula.
For example, if the base is given in inches and the height is given in centimeters, you need to convert one of the measurements to match the other. Once both measurements are in the same unit, you can proceed to calculate the area using the formula mentioned earlier.
| Base | Height | Area |
|---|---|---|
| 6 inches | 10 centimeters | 60 square inches (after converting height to inches) |
| 12 centimeters | 8 inches | 48 square centimeters (after converting base to centimeters) |
By converting the measurements to the same unit, we can accurately calculate the area of the parallelogram.
Now that you understand how to calculate the area of a parallelogram and handle different unit measurements, you can confidently apply this knowledge to solve geometry problems involving parallelograms.
Finding the Perimeter of a Parallelogram
Calculating the perimeter of a parallelogram is an essential skill in geometry. The perimeter is the distance around the outer edge of a shape, and for a parallelogram, it can be found by adding the lengths of all its sides.
To determine the perimeter of a parallelogram, you need to know the lengths of its opposite sides. Since a parallelogram has two pairs of equal-length sides, you can either add the lengths of two adjacent sides or multiply the length of one side by four.
Here’s the formula for finding the perimeter of a parallelogram:
Perimeter = 2 * (Side1 + Side2)
Let’s understand this better with an example:
Example:
Consider a parallelogram with a length of 8 units and a width of 5 units. To find its perimeter, we can use the formula:
Perimeter = 2 * (8 + 5) = 26 units
So, the perimeter of the given parallelogram is 26 units.
Understanding how to find the perimeter of a parallelogram is crucial for various real-life applications, such as calculating the amount of fencing required to enclose a parallelogram-shaped garden or determining the distance around a parallelogram-shaped track.
Now, let’s take a look at a table summarizing the perimeters of parallelograms with different side lengths:
| Parallelogram | Side 1 | Side 2 | Perimeter |
|---|---|---|---|
| Parallelogram 1 | 4 units | 6 units | 20 units |
| Parallelogram 2 | 9 units | 12 units | 42 units |
| Parallelogram 3 | 7 units | 7 units | 28 units |
As you can see from the examples in the table, the perimeter varies based on the lengths of the sides. By understanding the formula and practicing with different values, you can confidently find the perimeter of any parallelogram.
Conclusion
After exploring the unique properties of parallelograms and gaining a solid understanding of their geometry, you are now equipped to confidently solve geometry problems involving this fascinating shape. By understanding the angles, sides, area, and perimeter of a parallelogram, you have unlocked the key to unlocking its mysteries.
Throughout this article, we have seen how parallelograms are a type of quadrilateral with special properties that set them apart from other shapes. They have opposite sides that are parallel and congruent, as well as opposite angles that are congruent. These properties make parallelograms a versatile tool in geometry, allowing us to solve a wide range of problems.
Furthermore, we have learned how to calculate the area and perimeter of a parallelogram, using the appropriate formulas and applying them to practical examples. Understanding these calculations is crucial for real-world applications, such as determining the area of a field or the perimeter of a fence.
In conclusion, the study of parallelograms is essential for anyone interested in geometry. By mastering their properties, angles, sides, area, and perimeter, you are well-prepared to tackle more complex geometric concepts and problem-solving challenges. So, embrace the parallelogram and unlock its potential in your mathematical journey.
FAQ
What is a parallelogram?
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length.
What are the properties of a parallelogram?
The properties of a parallelogram include having opposite sides that are parallel and equal in length, opposite angles that are congruent, consecutive angles that are supplementary, and diagonals that bisect each other.
How do you find the area of a parallelogram?
To find the area of a parallelogram, you can multiply the length of the base by the height.
What is the formula for calculating the perimeter of a parallelogram?
The formula for calculating the perimeter of a parallelogram is to add up the lengths of all four sides.
How can I prove that a quadrilateral is a parallelogram?
You can prove that a quadrilateral is a parallelogram by showing that opposite sides are parallel and equal in length, opposite angles are congruent, or the diagonals bisect each other.
Can a parallelogram have right angles?
Yes, a parallelogram can have right angles. When a parallelogram has four right angles, it is called a rectangle.
Are all rectangles parallelograms?
Yes, all rectangles are parallelograms. A rectangle is a special type of parallelogram with four right angles.
Can a parallelogram have congruent diagonals?
Yes, a parallelogram can have congruent diagonals. In fact, the diagonals of a parallelogram bisect each other.
What is the sum of the angles in a parallelogram?
The sum of the angles in a parallelogram is always 360 degrees.
Are all squares parallelograms?
Yes, all squares are parallelograms. A square is a special type of parallelogram with four congruent sides and four right angles.